Calibration by correlation using metric embedding from non-metric similarities.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 35:2357–2370, 10 2013.
 pdfdoi
pdfdoi supp. material
supp. material
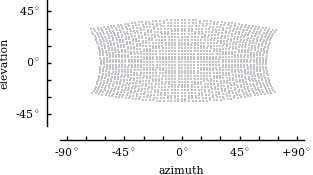
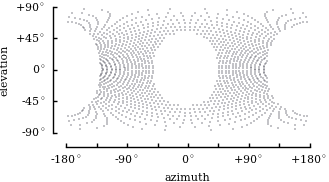
Abstract: This paper presents a new intrinsic calibration method that allows us to calibrate a generic single-view point camera just by waving it around. From the video sequence obtained while the camera undergoes random motion, we compute the pairwise time correlation of the luminance signal for a subset of the pixels. We show that, if the camera undergoes a random uniform motion, then the pairwise correlation of any pixels pair is a function of the distance between the pixel directions on the visual sphere. This leads to formalizing calibration as a problem of metric embedding from non-metric measurements: we want to find the disposition of pixels on the visual sphere, from similarities that are an unknown function of the distances. This problem is a generalization of multidimensional scaling (MDS) that has so far resisted a comprehensive observability analysis (can we reconstruct a metrically accurate embedding?) and a solid generic solution (how to do so?). We show that the observability depends both on the local geometric properties (curvature) as well as on the global topological properties (connectedness) of the target manifold. It follows that, in contrast to the Euclidean case, on the sphere we can recover the scale of the points distribution, therefore obtaining a metrically accurate solution from non-metric measurements. We describe an algorithm that is robust across manifolds and can recover a metrically accurate solution when the metric information is observable. We demonstrate the performance of the algorithm for several cameras (pin-hole, fish-eye, omnidirectional), and we obtain results comparable to calibration using classical methods. Additional synthetic benchmarks show that the algorithm performs as theoretically predicted for all corner cases of the observability analysis.
Supplemental Materials
Results as 3D Matlab figures (
.fig):- Flip Mino camera - small field of view (45deg)
- GOPRO camera - large field of view (150deg)
- omnidirectional camera (360deg)
- Python source code (.tgz); manual coming soon.
Example input data
Our method calibrates a camera just by considering the inter-pixel correlations when the camera undergoes random motion. These movies are some examples of the input data that we use for calibration in the paper (download the complete logs here). From these videos, and nothing else, we can reconstruct the sensor geometry for generic optics.
| camera |
Flip Mino 
|
GOPRO 
|
Omnidirectional camera 
|
| example log | |||
| place | Andrea walking in the Caltech campus | Davide walking in the streets of Philadelphia | Davide indoor shaking it like a polaroid picture |
| solution |
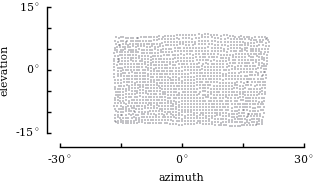
|
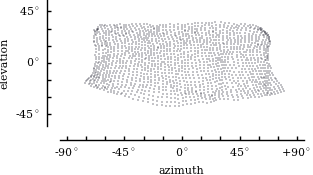
|
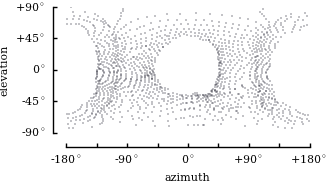
|
| ground truth |
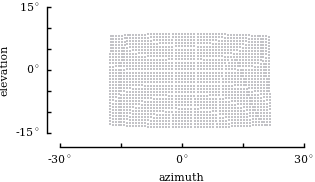
|
|
|
